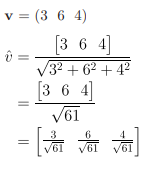Rangkuman Matematika Kelas 10 Bab 3 Kurikulum Merdeka
Kherysuryawan.id – Ringkasan materi matematika kelas 10 SMA/SMK Kurikulum Merdeka Bab 3 “Vektor dan Operasinya” Semester 1.
Sahabat kherysuryawan yang berbahagia,
bagaimana kaabr anda hari ini ? semoga kita semua selalu dalam keadaan sehat
sehingga dapat selalu melaksanakan aktivitas keseharian dengan baik. Oh ya pada
postingan kali ini kita akan berjumpa kembali pada pembahasan seputar materi
matematika yang ada di kelas 10 SMA/SMK Bab 3 tentang Vektor dan Operasinya
yang akan di pelajari di semester 1 kurikulum merdeka.
Melalui postingan ini admin akan
memberikan ringkasan materi matematika kelas 10 Bab 3 Vektor dan Operasinya
dengan harapan dapat membantu para siswa dan guru yang membutuhkan
rangkuman/ringkasan materi matematika kelas 10 Bab 3 kurikulum merdeka.
Untuk memudahkan siswa dalam belajar
matematika maka diharapkan bisa membuat atau menyiapkan ringkasan materi dari
setiap bab yang ada pada mata pelajaran matematika. Ringkasan materi akan
sangat membantu siswa dalam memudahkan untuk memahami materi yang sedang di
pelajari sebab ringkasan merupakan inti atau point penting yang ada pada
tiap-tiap materi.
Seperti kita ketahui bahwa materi yang
terdapat pada mata pelajaran matematika lumayan banyak khususnya di kelas 10
SMA/SMK sehingga untuk memudahkan dalam mempelajarinya maka kita dapat membuat
sebuah ringkasan materi dari sumber materi yang ada di buku teks pelajaran
matematika.
Nah di kesempatan kali ini admin telah
menyiapkan ringkasan/rangkuman materi untuk mata pelajaran matematika kelas 10
SMA/SMK khususnya pada Bab 3 tentang Vektor dan Operasinya yang nantinya akan
di pelajari di semester 1 kurikulum merdeka.
Ringkasan materi matematika kelas 10 Bab
3 Vektor dan Operasinya semester 1 kurikulum merdeka yang akan admin bagikan
ini seluruhnya bersumber dari buku siswa matematika kelas 10 SMA/SMK kurikulum
merdeka sehingga bagi anda yang di sekolahnya telah belajar dengan menggunakan
kurikulum merdeka maka bisa memanfaatkan materi ringkasan ini sebagai bahan
pembelajaran.
Ada beberapa sub materi yang nantinya
akan di pelajari di mata pelajaran matematika kelas 10 SMA/SMK Bab 3 Vektor dan
Operasinya pada kurikulum merdeka, diantaranya yaitu sebagai berikut :
1. Panjang dan Arah Vektor
2. Vektor Negatif atau Vektor Lawan
3. Vektor Ekuivalen (Vektor yang Sama)
B. Vektor dan Sistem Koordinat
1. Vektor Berdimensi Dua pada Sistem Koordinat
2. Komponen-Komponen Vektor
3. Vektor-Vektor Ekuivalen pada Sistem Koordinat Kartesius
4. Vektor Berdimensi Tiga pada Sistem Koordinat Kartesius
5. Vektor Kolom dan Vektor Baris
6. Vektor Satuan dari Suatu Vektor
7. Vektor Posisi
8. Vektor Berkebalikan
C. Operasi Vektor
1. Penjumlahan Vektor
a. Penjumlahan Dua Vektor dengan Metode Segitiga
b. Penjumlahan Dua Vektor dengan Metode Jajar Genjang
c. Penjumlahan dengan Metode Poligon
d. Penjumlahan Vektor secara Komponen
2. Pengurangan Vektor
3. Perkalian Skalar dengan Vektor
Baiklah untuk anda yang ingin melihat
lebih lengkap tentang ringkasan materi pelajaran matematika kelas 10 SMA/SMK Bab
3 “Vektor dan Operasinya” semester 1 kurikulum merdeka, maka silahkan di lihat
sajiannya di bawah ini:
Bab 3 Vektor dan Operasinya
A. Terminologi, Notasi, dan Jenis Vektor
Cara mengukur sudut adalah sebagai
berikut.
1. Panjang dan Arah Vektor
Kalian perhatikan vektor CD dengan
panjang 4 cm dan arahnya membentuk sudut 45o dengan horizontal. Kalian dapat
menyebutkan vektor CD dengan panjang 4 cm dan arah Timur Laut jika merujuk pada
arah mata angin.
2. Vektor Negaif atau Vektor Lawan
Andi berjalan sejauh 100 m dengan arah
30°, kemudian Andi kembali ke posisi semula.
Baca Juga
Vektor A menyatakan perpindahan Andi
yang pertama.
Vektor -A menyatakan perpindahan Andi
yang kedua.
Vektor A dan -A sama panjang tetapi
berlawanan arah.
-A adalah vektor lawan dari A.
Vektor negatif atau vektor lawan adalah
vektor dengan besar sama, tetapi arah berlawanan dengan suatu vektor.
Vektor Nol
Vektor nol adalah vektor dengan panjang
nol dan tidak punya arah tertentu atau vektor dengan titik pangkal dan ujung
yang sama. Vektor nol dinyatakan dengan titik secara grais.
Jika Andi berjalan sejauh 100 m ke timur
kemudian 100 m ke barat maka Andi mengalami perpindahan 0.
3. Vektor Ekuivalen (Vektor yang Sama)
Jika ada vektor lain dengan panjang 3 cm
dan sudut 45°, maka dikatakan vektor tersebut ekuivalen dengan vektor CD.
Ketiga vektor, dalam gambar diatas, sama
atau ekuivalen walaupun ketiganya mempunyai titik awal yang berbeda, sehingga
dapat dituliskan sebagai berikut.
CD = EF = KL
Vektor CD ekuivalen dengan vektor EF dan
vektor KL.
B. Vektor dan Sistem Koordinat
Perhatikan sistem koordinat Kartesius di
bawah ini.
Koordinat titik O adalah (0, 0) dan Q
adalah (x, y). Vektor satuan diperlukan untuk menunjukkan bagaimana mencapai
titik Q dari titik O.
i adalah vektor satuan dalam arah-x
(horizontal) dan j adalah vektor satuan dalam arah-y (vertikal). Vektor satuan
mempunyai besar 1 satuan. Arah horizontal negatif dinyatakan dengan -i dan arah
vertikal negatif dinyatakan dengan -j.
Vektor OQ dinyatakan sebagai berikut. OQ
= x i + y j
Ada dua komponen yang membentuk vektor
OQ, komponen horizontal dan komponen vertikal. Jika dari titik O arah komponen
horizontal adalah timur-barat, maka arah komponen vertikal adalah
utara-selatan. Komponen-x merupakan proyeksi ortogonal vektor pada sumbu-x.
Komponen-y merupakan proyeksi ortogonal vektor pada sumbu-y.
Vektor dengan dua komponen disebut
sebagai vektor berdimensi dua.
2. Komponen-Komponen Vektor
Berikut ini Vektor AB dan
Komponen-Komponennya
3. Vektor-Vektor Ekuivalen pada Sistem
Koordinat Kartesius
Perhatikan dua vektor perpindahan dalam
sistem koordinat di bawah ini.
Vektor u dan v ekuivalen, dinyatakan
dengan 4 i + 3 j, walau keduanya mempunyai koordinat titik pangkal dan
koordinat titik ujung yang berbeda. Komponen horizontal dan komponen vertikal
adalah 4 dan 3.
4. Vektor Berdimensi Tiga pada Sistem
Koordinat Kartesius
Vektor dengan tiga komponen, disebut
sebagai vektor berdimensi tiga. Jika dari titik O arah komponen horizontal
adalah timur-barat, arah komponen vertikal adalah utara-selatan, maka arah
satunya lagi adalah atas-bawah atau depan-belakang atau tegak lurus terhadap
bidang xy.
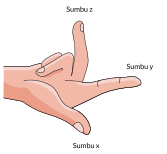
Sistem koordinat tiga dimensi dapat
diperagakan dengan tiga jari. Ibu jari menghadap ke kalian adalah sumbu-x, jari
telunjuk mengarah ke kanan adalah sumbu-y dan jari tengah mengarah ke atas
adalah sumbu-z.
5. Vektor Kolom dan Vektor Baris
Vektor yang dituliskan dalam bentuk
kolom adalah vektor kolom. Vektor yang dituliskan dalam bentuk baris adalah
vektor baris.
Komponen-komponen vektor kolom
dituliskan sebagai berikut.
6. Vektor Satuan dari Suatu Vektor
Contoh soal:
(Menentukan vektor satuan dari v)
7. Vektor Posisi
Vektor OA dan OB merupakan vektor
posisi, karena dimulai dari titik asal O dan berakhir di A dan B. Vektor posisi
selalu dimulai dari titik O dan berakhir pada suatu titik lain. Vektor posisi
OA dan OB adalah (–3 2) dan (7 5).
Vektor posisi adalah vektor yang
berpangkal di titik O yang merupakan pusat koordinat dan berujung di suatu
titik dalam sistem koordinat.
8. Vektor Berkebalikan
C. Operasi Vektor
1. Penjumlahan Vektor
a. Penjumlahan Dua Vektor dengan Metode
Segiiga
Penjumlahan vektor dapat dilakukan
dengan cara grais. Ujung vektor pertama bertemu dengan pangkal vektor kedua.
Hasilnya adalah vektor dengan pangkal vektor pertama dengan ujung vektor kedua.
Betuk penjumlahan adalah segitiga.
Penjumlahan vektor mengikuti sifat
komutatif a + b = b + a
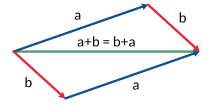
b. Penjumlahan Dua Vektor dengan Metode
Jajar Genjang
Penjumlahan vektor berkaitan dengan
bentuk jajar genjang.
c. Penjumlahan dengan Metode Poligon
Sifat komutatif tetap berlaku untuk
penjumlahan lebih dari dua vektor. Karena vektor hanya ditentukan oleh panjang
dan arahnya, maka dapat dipindahkan dengan leluasa. Penjumlahan secara grais
selalu dilakukan dengan cara ujung vektor sebelumnya bertemu dengan pangkal
vektor sesudahnya
d. Penjumlahan Vektor secara Komponen
Selain secara grais vektor juga dapat
dijumlahkan secara komponen.
AC + AB = (–3 3) + (4 2) = (1 5)
Penjumlahan secara komponen dan secara grais memberikan hasil yang sama.
2. Pengurangan Vektor
Salah satu cara menyelesaikan soal
pengurangan vektor dengan cara seperti yang ditunjukkan dalam gambar di bawah
ini. Arah vektor OB dibuat berlawanan dan dijumlahkan dengan vektor OA.
Pengurangan vektor dapat dilakukan
secara komponen. Perhatikan dua vektor di bawah ini.
AB – AC = AB + (–AC) = (4 2) + (3 –3) =
(7 –1)
Vektor Nol
Vektor nol adalah vektor dengan panjang
nol dan tidak punya arah tertentu atau vektor dengan titik pangkal dan ujung
yang sama. Vektor nol dinyatakan dengan titik secara grais.
Jika Andi berjalan sejauh 100 m ke timur
kemudian 100 m ke barat, maka Andi mengalami perpindahan 0.
3. Perkalian Skalar dengan Vektor
Vektor yang dikalikan dengan skalar
positif menghasilkan vektor dengan panjang berbeda.
Vektor yang dikalikan dengan skalar
negatif menghasilkan vektor dengan panjang dapat berbeda dan arah berlawanan.
Demikianlah ringkasan materi matematika
kelas 10 SMA/SMK Bab 3 “Vektor dan Operasinya” yang dapat admin berikan pada
kesempatan kali ini. Semoga dengan ringkasan materi tersebut maka dapat
membantu siswa maupun guru yang ingin mempelajari lebih dalam tentang Vektor
dan Operasinya.
Sekian dan semoga bermanfaat.