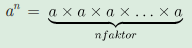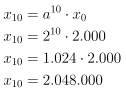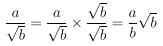Rangkuman Matematika Kelas 10 Bab 1 Kurikulum Merdeka

Kherysuryawan.id – Rangkuman materi matematika kelas 10 SMA/SMK Bab 1 “Eksponen dan Logaritma” pembelajaran semester 1 kurikulum merdeka.

Halo sahabat kherysuryawan, pada postingan kali ini admin akan membahas tentang salah satu materi yang ada pada mata pelajaran matematika di kelas 10 SMA/SMK kurikulum merdeka.

 

Seperti kita ketahui bahwa materi yang terdapat pada mata pelajaran matematika lumayan banyak khususnya di kelas 10 SMA/SMK sehingga untuk memudahkan dalam mempelajarinya maka kita dapat membuat sebuah ringkasan materi dari sumber materi yang ada di buku teks pelajaran matematika.

 

Nah di kesempatan kali ini admin telah menyiapkan ringkasan/rangkuman materi untuk mata pelajaran matematika kelas 10 SMA/SMK khususnya pada Bab 1 tentang Eksponen dan Logaritma yang nantinya akan di pelajari di semester 1 kurikulum merdeka.

 

Admin membuat ringkasan materi matematika kelas 10 bab 1 “Eksponen dan Logaritma” ini dengan tujuan agar dapat memudahkan bagi siswa yang ingin menggunakannya sebagai bahan belajar baik untuk belajar di rumah maupun di sekolah.

 

Ringkasan materi matematika kelas 10 Bab 1 Eksponen dan Logaritma semester 1 kurikulum merdeka yang akan admin bagikan ini seluruhnya bersumber dari buku siswa matematika kelas 10 SMA/SMK kurikulum merdeka sehingga bagi anda yang di sekolahnya telah belajar dengan menggunakan kurikulum merdeka maka bisa memanfaatkan materi ringkasan ini sebagai bahan pembelajaran.

 

Ada beberapa sub materi yang nantinya akan di pelajari di mata pelajaran matematika kelas 10 SMA/SMK Bab 1 Eksponen dan Logaritma pada kurikulum merdeka, diantaranya yaitu sebagai berikut :

 A. Eksponen

1. Deinisi Eksponen

2. Sifat-sifat Eksponen

3. Fungsi Eksponen

a. Pertumbuhan Eksponen

b. Peluruhan Eksponen

4. Bentuk Akar

a. Hubungan Bilangan Pangkat dan Akar

b. Merasionalkan Bentuk Akar

Baiklah untuk anda yang ingin melihat lebih lengkap tentang ringkasan materi pelajaran matematika kelas 10 SMA/SMK Bab 1 “Eksponen dan Logaritma” semester 1 kurikulum merdeka, maka silahkan di lihat sajiannya di bawah ini:

 

Bab 1 Eksponen dan Logaritma

A. Eksponen

Perkalian berulang adalah perkalian yang dilakukan secara berulang dengan faktor yang sama.

Perhatikan contoh berikut ini.

1. 2×2×2×2×2×2 ditulis dengan 2⁶

2. 5×5×5×5×5×5×5×5 ditulis dengan 5⁸

3. 15×15×15×15 ditulis dengan 15⁴

4. 7×7×7×7×7×7×7×7×7×7 ditulis dengan 7¹⁰

5. a×a×a×a×a×a×a ditulis dengan a⁷

 

1. Deinisi Eksponen

Jadi, banyaknya orang yang tertular pada setiap fase adalah perkalian bilangan 2 sebanyak “fase ke-“ kali.

Jika kalian mencari banyak orang yang tertular pada fase ke-5, maka banyak orang yang tertular sama dengan 2⁵ = 32 orang.

 

Jika banyak orang yang tertular pada fase ke-n dinyatakan dengan m, maka berdasarkan eksplorasi di atas m dapat dinyatakan dalam n sebagai m(n) yaitu: m(n) = 2ⁿ

 

Bentuk 2¹ , 2² , 2³ , 2⁴ dan 2ⁿ ini merupakan bentuk bilangan pangkat.

Bilangan berpangkat atau disebut juga eksponen dideinisikan sebagai berikut.

Jika a adalah bilangan real dan n adalah bilangan bulat positif, maka a n menyatakan hasil kali bilangan a sebanyak n faktor dan ditulis dengan :

Berikut adalah beberapa deinisi penting yang perlu di ketahui.

2. Sifat-sifat Eksponen

Berikut sifat-sifat eksponen yang perlu di ketahui.

Contoh:

 

3. Fungsi Eksponen

Deinisi Fungsi Eksponen

Sebuah fungsi eksponen dinyatakan dengan

f(x) = n × a^x

di mana a adalah bilangan pokok, a > 0, a ≠ 1, n adalah bilangan real tak nol dan x adalah sebarang bilangan real.

berikut ini contoh fungsi eksponen

1. f(x) = 4^x

2. f(x) = 3^x+1

 

Grafik fungsi eksponen pada f(x) = 3^x ditunjukkan pada gambar di bawah ini

Fungsi eksponen dibedakan menjadi dua bentuk, yaitu pertumbuhan eksponensial dan peluruhan eksponensial.

 

a. Pertumbuhan Eksponen

Fungsi pertumbuhan eksponen dituliskan dengan:

f(x) = a^x dengan a > 1

Contoh :

Seorang peneliti mengamati pertumbuhan bakteri selama beberapa jam. Setelah diamati, bakteri tersebut membelah menjadi n bakteri setiap jam. Setelah diamati, jumlah bakteri pada 2 jam pertama adalah 8.000 bakteri. Dua jam kemudian jumlah bakteri sudah mencapai 32.000 bakteri. Berapakah jumlah bakteri setelah 10 jam?

 

Jawaban:

Misalkan x₀ adalah banyaknya bakteri pada waktu t = 0.

Jika a adalah banyaknya bakteri setelah pembelahan setiap jam, maka

Untuk t = 0, banyak bakteri = x₀;

Untuk t = 1, banyak bakteri = a¹. x₀;

Untuk t = 2, banyak bakteri = a². x₀;

Untuk t = 3, banyak bakteri = a³. x₀;

Untuk t = 4, banyak bakteri = a⁴. x₀;

dan seterusnya.

Kalian harus mencari nilai a terlebih dahulu untuk mengetahui banyak bakteri yang dihasilkan ketika sebuah bakteri membelah dalam 1 jam. Jika banyak bakteri pada 2 jam pertama adalah x₂ dan banyak bakteri pada 2 jam berikutnya (4 jam kemudian) adalah x₄ , maka:

Jadi, setiap 1 jam bakteri akan membelah menjadi dua bakteri.

Selanjutnya kalian akan mencari banyak bakteri di awal yaitu x₀ Kalian bisa menggunakan persamaan x₂ = a2 .x₀ Substitusikan nilai a = 2 pada x₂ = a² .x₀

Jadi, banyaknya bakteri mula-mula adalah 2.000 bakteri.

Untuk mencari banyak bakteri pada 10 jam kemudian, maka digunakan persamaan x₁₀ = a¹⁰ .x0 . substitusikan nilai a = 2 dan x₀ = 2.000 pada x₁₀ = a¹⁰ .x₀.

Jadi, banyaknya bakteri setelah 10 jam adalah 2.048.000 bakteri.

 

b. Peluruhan Eksponen

Fungsi eksponen tidak hanya menggambarkan pertumbuhan yang signiikan dari waktu ke waktu. Fungsi eksponen juga menggambarkan penurunan secara konsisten pada periode waktu tertentu. Ini disebut peluruhan eksponen.

 

Fungsi peluruhan eksponen dapat dituliskan sebagai

f(x ) = n × a^x, dengan 0 < a < 1, n bilangan real tak nol, x adalah sebarang bilangan real.

 

Contoh:

Obat penahan rasa sakit disuntikkan kepada pasien yang mengalami luka berat akibat kecelakaan. Dosis obat yang disuntikkan adalah 50 mikrogram. Satu jam setelah penyuntikan, setengah dosis tersebut akan luruh dan dikeluarkan dari dalam tubuh. Proses tersebut akan terus berulang setiap jam.

1.       Berapa banyak dosis obat yang masih tertinggal di dalam tubuh pasien setelah 1 jam, 2 jam, dan 3 jam?

2.       Bagaimana model matematika yang dapat menyatakan peluruhan dosis obat tersebut?

 

Jawaban:

1. Dosis awal = 50 mikrogram

Misalkan dosis pada x waktu dilambangkan dengan f(x), maka

Jadi, dosis pada 1 jam pertama tersisa 25 mikrogram, pada 2 jam pertama tersisa 12,5 mikrogram, dan setelah 3 jam tersisa 6,25 mikrogram.

2. Berdasarkan bagian a, fungsi eksponen yang dapat menyatakan peluruhan dosis obat tersebut dari dalam tubuh pasien pada jam tertentu adalah f(x) = 50(1/2)^x  dengan x adalah waktu yang dibutuhkan obat tersebut untuk meluruh sebanyak setengah dosis dari dosis sebelumnya.

 

4. Bentuk Akar

a. Hubungan Bilangan Pangkat dan Akar

Contoh

b. Merasionalkan Bentuk Akar

Untuk merasionalkan bentuk akar, maka yang dapat dilakukan adalah dengan mengalikannya dengan bentuk akar sekawannya.

 

B. Logaritma

1. Deinisi Logaritma

Misalkan a adalah bilangan positif dengan 0 < a < 1 atau a > 1, b > 0,

^a log b = c jika dan hanya jika b = a^c

Di mana,

a adalah bilangan pokok atau basis logaritma

b adalah numerus

c adalah hasil logaritma

Jadi, antara eksponen dan logaritma saling terkait. Logaritma adalah inversi atau kebalikan dari eksponen.

 

Contoh Bentuk Eksponen dan Bentuk Logaritma disajikan pada yabel di bawah ini:

Bentuk logaritma yang juga perlu kalian ketahui adalah logaritma dengan basis 10 yang biasa disebut dengan Logaritma Umum.

 

Definisi Logaritma Umum

Logaritma yang memiliki basis 10 disebut dengan logaritma umum dan dituliskan sebagai berikut:

¹⁰ log a = log a

 

2. Sifat-sifat Logaritma

Berikut ini Sifat-sifat logaritma

Contoh 1:

Contoh 2:

 

Demikianlah ringkasan materi matematika kelas 10 SMA Bab 1 tentang Eksponen dan Logaritma yang bisa admin bagikan pada kesempatan kali ini. Semoga sajian materi diatas dapat membantu rekan-rekan pendidikan yang ingin lebih mendalami materi tentang Eksponen dan Logaritma yang nantinya akan di pelajari di kelas 10 kurikulum merdeka.

Share this post