Rangkuman Matematika Kelas 7 Bab 4 Kurikulum Merdeka
Kherysuryawan.id – Rangkuman Materi Matematika Kelas 7 SMP Kurikulum Merdeka Bab 4 “Perbandingan Senilai dan Perbandingan Berbalik Nilai” yang akan di pelajari pada pembelajaran di kurikulum merdeka.
Sahabat kherysuryawan, mata pelajaran
matematika merupakan mata pelajaran yang sangat penting untuk di pelajari oleh
siswa di setiap jenjang pendidikan.
Meskipun mata pelajaran matematika
sering dianggap sebagai mata pelajaran yang menakutkan bagi sebagian siswa di
sekolah namun sebenarnya mempelajari matematika akan menjadi sangat asyik dan
menarik apabila kita bisa memahami materi yang sedang di pelajari.
Nah untuk bisa memudahkan siswa dalam
memahami materi pelajaran matematika tentunya ada banyak cara yang bisa di
lakukan. Salah satunya ialah dengan membuat ringkasan atau rangkuman materi
dari buku teks pelajaran matematika yang sedang di pelajari.
Membuat ringkasan atau rangkuman materi
akan semakin memudahkan kita dalam menyerap dan memahami materi sebab materi
yang akan kita pelajari telah di sederhanakan dan hanya menampilkan materi yang
dianggap penting saja sehingga kita tidak terlalu banyak menghabiskan waktu
untuk belajar.
Pada kesempatan kali ini admin
kherysuryawan akan membantu para peserta didik yang ingin mudah dalam belajar
matematika yakni dengan mempelajari ringkasan/rangkuman materi matematika. Di kesempatan
ini admin akan berbagi ringkasan materi matematika untuk kelas 7 SMP khususnya
materi yang ada pada Bab 4 yaitu tentang “Perbandingan Senilai dan Perbandingan
Berbalik Nilai” yang akan di pelajari pada pembelajaran di kurikulum merdeka.
Perlu di ketahui bahwa pada mata
pelajaran matematika kelas 7 kurikulum merdeka khususnya pada bab 4 “Perbandingan
Senilai dan Perbandingan Berbalik Nilai” ada beberapa sub materi yang nantinya
akan di pelajari. Berikut ini sub materi yang akan di pelajari pada mata
pelajaran matematika kelas 7 bab 4 “Perbandingan Senilai dan Perbandingan
Berbalik Nilai”.
A. Fungsi
B. Perbandingan Senilai
C. Perbandingan Berbalik Nilai
D. Menerapkan Perbandingan Senilai dan Perbandingan Berbalik Nilai
Baiklah berikut ini sajian lengkap
ringkasan/rangkuman materi matematika kelas 7 Bab 4 “Perbandingan Senilai dan
Perbandingan Berbalik Nilai” yang akan di pelajari pada kurikulum merdeka.
BAB 4: PERBANDINGAN SENILAI DAN PERBANDINGAN BERBALIK NILAI
1. Fungsi
Sebuah jendela geser berbentuk persegi panjang dengan tinggi 90 cm. Misalkan x cm adalah lebar, dan y cm adalah keliling bagian terbuka dari jendela tersebut. Mari gunakan tabel di bawah ini untuk merangkum hubungan antara x dan y.
Huruf-huruf, seperti x dan y, yang
menyajikan nilai-nilai yang berbeda disebut variabel atau peubah.
Jika sepasang variabel x dan y berubah
bersamaan seperti pada tampilan diatas dan jika untuk suatu nilai x yang
ditetapkan hanya ada satu nilai y yang bersesuaian, maka dikatakan y adalah
fungsi dari x. Keliling merupakan fungsi dari lebar bagian terbuka jendela pada
gambar diatas.
Contoh :
Misalkan y cm2 adalah luas
bagian terbuka jendela (gambar diatas) . Jika jendela dibuka 10 cm, maka luas
bagian terbuka adalah 900 cm2 . Secara umum, jika untuk suatu nilai
x yang ditetapkan terdapat tepat satu nilai y, maka y adalah fungsi dari x.
2. Perbandingan Senilai
Perbandingan Senilai dan Persamaan
Jika y adalah fungsi dari x dan hubungan
antara variabel x dan y dinyatakan sebagai
y = ax
maka dikatakan bahwa y berbanding lurus
dengan x. Perlu diperhatikan bahwa a adalah konstanta yang tidak boleh 0. Dalam
hal ini, a disebut konstanta perbandingan.
Contoh:
Diberikan kawat dengan berat 20 g per
meter. Berat x meter adalah y g. Jika y dinyatakan dalam x dengan persamaan,
maka
y = 20x.
Jadi, y berbanding lurus terhadap x, dan
konstanta perbandingannya adalah 20.
Menyusun Persamaan Perbandingan
Senilai
Contoh:
Diketahui bahwa y berbanding lurus
dengan x, dan ketika x = 2, maka y = –8. Nyatakanlah y dalam x menggunakan
persamaan. Selain itu, tentukan nilai y ketika x = –5.
Jawaban:
Koordinat dan Grafik Perbandingan
Senilai
v koordinat
Posisi titik-titik pada bidang dapat
dinyatakan sebagai pasangan bilangan.
Kita dapat menggunakan langkah-langkah
berikut ini untuk menentukan posisi titik-titik dengan perluasan ke
bilangan-bilangan negatif. Buatlah dua garis saling tegak lurus terlebih
dahulu, seperti ditunjukkan pada gambar di samping. Garis bilangan horisontal
kita sebut sumbu x atau sumbu Temukan contoh seperti kalimat di atas di
sekitarmu. horisontal. Garis bilangan vertikal kita sebut sumbu y, atau sumbu
vertikal. Sumbu x dan sumbu y bersama[1]sama kita sebut sumbu
koordinat. Titik potong antara kedua sumbu disebut titik pangkal. Arah positif
sumbu x adalah ke kanan, adapun arah positif sumbu y adalah ke atas.
Posisi titik A dapat ditunjukkan pada
gambar berikut ini.
Gambarlah dua garis saling tegak lurus
dari titik A ke sumbu x dan sumbu y, berikan tanda pada titik potongnya pada
sumbu x dan sumbu y. Dengan demikian, posisi titik A dapat dinyatakan sebagai
pasangan bilangan (2, 3).
Kita katakan bahwa 2 adalah absis dari A
dan 3 adalah ordinat dari A. (2, 3) adalah koordinat dari A. Titik A dapat
dinyatakan sebagai (2, 3).
v Grafik Perbandingan Senilai
Kita dapat menggunakan tabel berikut ini
untuk menjelaskan fungsi y = 2x.
Gunakanlah pasangan-pasangan nilai-nilai
x dan y pada tabel di atas sebagai absis dan ordinat, misalnya (–5, –10), …,
(5, 10), kemudian gambarlah titik-titik tersebut.
Seperti ditunjukkan pada gambar di bawah
ini yang sebelah kiri, jika kita tambah banyaknya titik-titik dengan koordinat
merupakan pasangan x dan y pada y = 2x, maka kumpulan titik-titik akhirnya akan
membentuk sebuah garis seperti yang ditunjukkan pada gambar di sebelah kanan
bawah. Garis ini disebut grafik fungsi y = 2x.
Berikut ini kesimpulan tentang grafik
perbandingan senilai:
Karena grafik perbandingan senilai
merupakan garis yang melalui titik pangkal, maka kita dapat menggambarkannya
jika kita mengetahui titik pangkal O dan satu titik pada grafik.
Contoh:
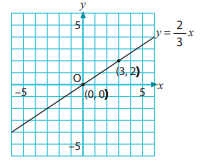
Pada fungsi y = 2/3 x, ketika x = 3, y =
2, grafik melalui titik (0, 0) dan (3, 2).
3. Perbandingan Berbalik Nilai
v
Perbandingan Berbalik Nilai dan
Persamaan
Berikut ini informasi pening tentang
perbandingan berbalik nilai:
Jika y berbanding terbalik dengan x,
maka hasil kali xy tetap. Nilainya merupakan konstanta perbandingan a.
Contoh:
y berbanding terbalik dengan x, dan
ketika x = 12, maka y = 6. Nyatakanlah y dalam x menggunakan persamaan. Berapa
nilai y ketika x = 9?
Jawaban:
v Grafik Perbandingan Berbalik Nilai
Berikut ini informasi penting tentang
grafik perbandingan berbalik nilai:
4. Menerapkan Perbandingan Senilai dan Perbandingan
Berbalik Nilai
Contoh 1:
Sebuah benda seni terbuat dari kawat
seberat 80 gram. Segulung kawat sejenis beratnya 54 gram dan panjangnya 3 m.
Berapakah panjang kawat yang dipakai untuk membuat benda seni tersebut?
Jawaban:
1) Membentuk persamaan berdasarkan yang diketahui, yaitu panjang kawat
berbanding lurus dengan beratnya
2) Gunakan kalimat perbandingan untuk menyatakan berat dan panjang kawat.
Contoh 2:
Diketahui sebuah persegi ABCD seperti
ditunjukkan pada gambar di atas. Titik P bergerak dari titik A sepanjang sisi
AB. Jika AP adalah x cm dan luas segitiga APD adalah y cm2 , dapatkah
disimpulkan bahwa y berbanding lurus dengan x? Atau dapatkah disimpulkan y
berbanding terbalik dengan x?
Jawaban:
Contoh 3:
Dua bersaudara berangkat dari rumah bersama-sama
menuju stasiun kereta yang jaraknya 1.200 m. Untuk setiap anak, y adalah jarak
yang telah ditempuh x menit setelah berangkat. Grafik di bawah ini menunjukkan
hubungan antara x dan y untuk anak yang lebih tua (kakak). Hitunglah kecepatan
berjalan kakak.
Jawaban:
Demikianlah penjelasan seputar ringkasan materi matematika kelas 7 SMP Bab 4 tentang “Perbandingan Senilai dan Perbandingan Berbalik Nilai” pada pembelajaran di kurikulum merdeka yang dapat admin sajikan. Semoga seluruh ringkasan materi diatas dapat menjadi salah satu sumber belajar matematika untuk kelas 7 SMP agar siswa dapat lebih mudah dalam memahami materi pelajaran.