Rangkuman Materi matematika Kelas 12 Bab 1 Dimensi Tiga
Kherysuryawan.id – Ringkasan materi matematika kelas XII Bab 1 tentang Dimensi Tiga yang akan di pelajari di semester 1.
Sahabat pendidikan, pada kesempatan kali
ini admin akan membahas seputar materi matematika yang terdapat di kelas `12
SMA. Adapun materi yang akan di ulas yakni materi yang terdapat pada Bab 1
tentang dimensi tiga.
Meskipun di sekolah telah disiapkan buku
paket pelajaran berupa buku siswa namun untuk bisa lebih mudah dalam memahami keseluruhan
materi yang terdapat didalam buku pelajaran tersebut dibutuhkan waktu yang
cukup lama sehingga sebagai seorang siswa yang kreatif maka harus bisa membuat
sebuah rangkuman atau ringkasan materi yang tentunya akan memudahkan dalam
proses belajar.
Membuat rangkuman materi atau ringkasan
materi sudah menjadi hal biasa yang sering di lakukan baik oleh guru maupun
oleh siswa. Hal tersebut di lakukan untuk lebih memaksimalkan waktu dalam mempelajari
materi yang ada. Rangkuman tentunya memuat materi-materi yang penting saja
sehingga akan lebih mudah dipelajari dengan tujuan agar lebih mudah untuk di
pahami.
Nah, kali ini admin akan mencoba untuk
bisa membagikan ringkasan/rangkuman materi untuk mata pelajaran matematika
kelas 12 SMA semester 1 khususnya materi yang ada pada bab 1 yaitu tentang
dimensi tiga.
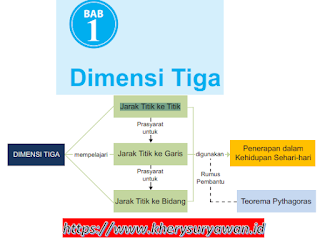
Pada materi matematika kelas 12 Bab 1 dimensi
tiga, ada tiga point penting yang nantinya akan di pelajari didalmnya, yaitu
sebagai berikut ;
1. Jarak Titik ke Titik
2. Jarak Titik ke garis
3. Jarak Titik ke bidang
Baiklah bagi anda yang membutuhkan
ringkasan materi untuk mata pelajaran matematika kelas 12 Bab 1 tentang dimensi
tiga yang akan membahas ketiga materi diatas, maka anda bisa melihat sajian
ringkasan materinya yang akan di siapkan di bawah ini ;
Jarak Antar titik
Perhatikan bangun ruang berikut ini.
Bangun 1.1.a merupakan kubus ABCD.EFGH
dengan panjang rusuk = 3 cm. EC, EG, dan AC, masing-masing merupakan jarak
antara titik E dengan C, titik E dengan G, serta titik A dengan titik C. Pada
Bangun 1.1.b jarak antara titik P dan Q adalah panjang ruas garis PQ.
Contoh :
Dalam suatu kamar berukuran 4m × 4m × 4m
dipasang lampu tepat di[1]tengah-tengah atap.
Kamar tersebut digambarkan sebagai kubus ABCD. EFGH. Berapa jarak lampu ke
salah satu sudut lantai kamar?
Alternatif Penyelesaian
Misal kamar tersebut digambarkan sebagai
kubus ABCD.EFGH dan lampu dinyatakan dengan titik T seperti berikut.
Jarak lampu ke salah satu sudut lantai
kamar adalah jarak titik T ke titik A atau titik B atau titik C atau titik D.
Titik T merupakan titik tengah bidang EFGH, sehingga TA = TB = TC = TD. Akan
dicari jarak titik T ke titik A. Jarak titik T ke titik A salah satunya dapat
dicari dari segitiga AET. Karena garis AE tegak lurus dengan garis ET , maka
segitiga AET merupakan segitiga siku-siku yang siku-siku di E. Dengan
menggunakan Teorema Pythagoras diperoleh AT2 = AE2 + ET2
Menentukan panjang Garis ET
Oleh karena T merupakan titik tengah,
maka ET = 1/2 EG.
Karena EG merupakan diagonal bidang,
Mengonstruksi Rumus Jarak Antar Titik
Radar (dalam bahasa inggris merupakan
singkatan dari Radio Detection and Ranging) adalah suatu sistem gelombang
elektromagnetik yang berguna untuk mendeteksi, mengukur jarak dan membuat peta
benda-benda seperti pesawat terbang, kapal laut, berbagai kendaraan bermotor
dan informasi cuaca. Radar dapat mendeteksi posisi suatu benda melalaui layar
seperti berikut.
Titik dalam radar tersebut merepresentasikan
objek yang dideteksi radar. Titik pusat radar adalah lokasi sinyal radar
dipancarkan.
Jarak Titik ke Garis
Perhatikan Jarak titik ke garis pada
bangun ruang.
Contoh:
Diberikan kubus ABCD.EFGH sebagai
berikut.
Jika panjang rusuk kubus adalah 2 cm, berapakah jarak titik A ke diagonal bidang ruas garis EB ?
Alternatif Penyelesaian
Jika titik E dan B dihubungkan dengan
ruas garis, maka diperoleh,
Jarak Titik ke Bidang
Untuk lebih memahami tentang jarak titik
ke bidang amatilah tabel berikut.
Contoh :
Diberikan kubus ABCD.EFGH dengan panjang
rusuk 4 cm. Titik A, F, G, dan D dihubungkan sehingga terbentuk bidang AFGD
seperti gambar di samping. Berapakah jarak titik B ke bidang AFGD?
Alternatif Penyelesaian
Untuk menentukan jarak titik B ke bidang
AFGD dapat ditentukan dengan mencari panjang ruas garis yang tegak lurus dengan
bidang AFGD dan melalui titik B.
Demikianlah ringkasan/rangkuman materi
matematika kelas 12 Bab 1 tentang Dimensi Tiga yang mempelajari tentang Jarak
Titik ke Titik, Jarak Titik ke garis dan Jarak Titik ke bidang. Ringkasan
materi diatas kiranya bisa membantu para siswa untuk memudahkan dalam proses
memahami materi matematika yang ada di pelajaran Bab 1.
Sekian dan Terimakasih